lunes

CADENAS DE MARKOV

En la teoría de la probabilidad, se conoce como cadena de Márkov a un tipo especial de proceso estocástico discreto en el que la probabilidad de que ocurra un evento depende del evento inmediatamente anterior. En efecto, las cadenas de este tipo tienen memoria. "Recuerdan" el último evento y esto condiciona las posibilidades de los eventos futuros. Esta dependencia del evento anterior distingue a las cadenas de Márkov de las series de eventos independientes, como tirar una moneda al aire o un dado.


En matemáticas, se define como un proceso estocástico discreto que cumple con la propiedad de Márkov, es decir, si se conoce la historia del sistema hasta su instante actual, su estado presente resume toda la información relevante para describir en probabilidad su estado futuro.
Una cadena de Márkov es una secuencia X1, X2, X3,... de variables aleatorias. El rango de estas variables, es llamado espacio estado, el valor de Xn es el estado del proceso en el tiempo n. Si la distribución de probabilidad condicional de Xn+1 en estados pasados es una función de Xn por sí sola, entonces:
P(X_{n+1}=x_{n+1}|X_n=x_n, X_{n-1}=x_{n-1}, \ldots, X_2=x_2, X_1=x_1) = P(X_{n+1}=x_{n+1}|X_n=x_n). \,
Donde xi es el estado del proceso en el instante i. La identidad mostrada es la propiedad de Márkov.


Tipos de cadenas de Markov

Cadenas irreducibles

Una cadena de Markov se dice irreducible si se cumple cualquiera de las siguientes condiciones (equivalentes entre sí):
1. Desde cualquier estado de E se puede acceder a cualquier otro.
2. Todos los estados se comunican entre sí.
3. C(x)=E para algún x∈E.
4. C(x)=E para todo x∈E.
5. El único conjunto cerrado es el total.
La cadena de Ehrenfest o la caminata aleatoria sin barreras absorbentes son ejemplos de cadenas de Markov irreducibles.


Cadenas positivo-recurrentes

Una cadena de Markov se dice positivo-recurrente si todos sus estados son positivo-recurrentes. Si la cadena es además irreducible es posible demostrar que existe un único vector de probabilidad invariante y está dado por:
\pi_x = 1/\mu_x \,


Cadenas regulares

Una cadena de Markov se dice regular (también primitiva o ergódica) si existe alguna potencia positiva de la matriz de transición cuyas entradas sean todas estrictamente mayores que cero.
Cuando el espacio de estados E es finito, si P denota la matriz de transición de la cadena se tiene que:
\lim_{n \to \mathcal{1} \,}P^n= W
donde W es una matriz con todos sus renglones iguales a un mismo vector de probabilidad w, que resulta ser el vector de probabilidad invariante de la cadena. En el caso de cadenas regulares, éste vector invariante es único.


Cadenas absorbentes

Una cadena de Markov con espacio de estados finito se dice absorbente si se cumplen las dos condiciones siguientes:
1. La cadena tiene al menos un estado absorbente.
2. De cualquier estado no absorbente se accede a algún estado absorbente.
Si denotamos como A al conjunto de todos los estados absorbentes y a su complemento como D, tenemos los siguientes resultados:
  • Su matriz de transición siempre se puede llevar a una de la forma
P = \begin{pmatrix} Q & R \\ 0 & I \end{pmatrix}
donde la submatriz Q corresponde a los estados del conjunto D, I es la matriz identidad, 0 es la matriz nula y R alguna submatriz.

  • P_x(T_A < \mathcal{1} \,) = 1 , esto es, no importa en donde se encuentre la cadena, eventualmente terminará en un estado absorbente.


Cadenas de Markov en tiempo continuo

Si en lugar de considerar una secuencia discreta X1, X2,..., Xi,.. con i indexado en el conjunto \mathbb{N}\;\! de números naturales, se consideran las variables aleatorias Xt con t que varía en un intervalo continuo del conjunto \mathbb{R}\;\! de números reales, tendremos una cadena en tiempo continuo. Para este tipo de cadenas en tiempo continuo la propiedad de Márkov se expresa de la siguiente manera:
P(X(t_{n+1})=x_{n+1} | X(t_n)=x_n, \ldots, X(t_1)=x_1) = P(X(t_{n+1})=x_{n+1}|X(t_n)=x_n) tal que  t_{n+1} > t_n > t_{n-1} > \dots > t_1
Formulación de las cadenas de Markov.
    Una cadena de Markov es una serie de eventos, en la cual la probabilidad de que ocurra un evento depende del evento inmediato anterior. En efecto, las cadenas de este tipo tienen memoria. " Recuerdan" el último evento y esto condiciona las posibilidades de los eventos futuros. Esta dependencia del evento anterior distingue a las cadenas de Markov de las series de eventos independientes, como tirar una moneda al aire o un dado.
 
    En la figura 4.1.1 se muestra el proceso para formular una cadena de Markov. El generador de Markov produce uno de n eventos posibles, Ej , donde j = 1, 2, . . . , n, a intervalos discretos de tiempo (que no tiene que ser iguales ). Las probabilidades de ocurrencia para cada uno de estos eventos depende del estado del generador. Este estado se describe por el último evento generado. En la figura 4.1.1, el último evento generado fue Ej , de manera que el generador se encuentra en el estado Mj .
image43_1.gif (2758 bytes)
    La probabilidad de que Ek sea el siguiente evento generado es una probabilidad condicional : P ( Ek / Mj ). Esto se llama probabilidad de transición del estado Mj al estado Ek. Para describir completamente una cadena de Markov es necesario saber el estado actual y todas las probabilidades de transición.
 
Probabilidades de transición.
 
    Una forma de describir una cadena de Markov es con un diagrama de estados, como el que se muestra en la figura 4.1.2. En ésta se ilustra un sistema de Markov con cuatro estados posibles : M1, M2 , M3 y M4 . La probabilidad condicional o de transición de moverse de un estado a otro se indica en el diagrama
image43_2.gif (2678 bytes)
    Otro método para exhibir las probabilidades de transición es usar una matriz de transición. . La matriz de transición para el ejemplo del diagrama de estados se muestra en la tabla 4.1.1 .
image43_3.gif (2720 bytes)
Otro método para exhibir las probabilidades de transición es usar una matriz de transición. .
Para n = 0, 1, 2, ....
 
El superíndice n no se escribe cuando n = 1.
Procesos estocásticos.
    Un proceso estocástico se define sencillamente como una colección indexada de variables aleatorias { X1 }, donde el subíndice t toma valores de un conjunto T dado. Con frecuencia T se toma como el conjunto de enteros no negativos y X, representa una característica de interés medible en el tiempo t. Por ejemplo, el proceso estocástico, X1 , X2 , X3, .., Puede representar la colección de niveles de inventario semanales (o mensuales) de un producto dado, o puede representar la colección de demandas semanales (o mensuales) de este producto.     Un estudio del comportamiento de un sistema de operación durante algún periodo suele llevar al análisis de un proceso estocástico con la siguiente estructura. En puntos específicos del tiempo t , el sistema se encuentra exactamente en una de un número finito de estados mutuamente excluyentes y exhaustivos, etiquetados 0, 1, . . , S. Los periodos en el tiempo pueden encontrarse a intervalos iguales o su esparcimiento puede depender del comportamiento general del sistema en el que se encuentra sumergido el proceso estocástico. Aunque los estados pueden constituir una caracterización tanto cualitativa como cuantitativa del sistema, no hay pérdida de generalidad con las etiquetas numéricas 0, 1, . . , M , que se usarán en adelante para denotar los estados posibles del sistema. Así la representación matemática del sistema físico es la de un proceso estocástico {Xi}, en donde las variables aleatorias se observan en t = 0, 1, 2,. . ., y en donde cada variable aleatoria puede tomar el valor de cualquiera de los M + 1 enteros 0, 1, .. , M . Estos enteros son una caracterización de los M + 1 estados del proceso
Propiedad Markoviana de 1o. orden .
    Se dice que un proceso estocástico tiene la propiedad markoviana si
P { Xt+1 = j | X0 = K0 , X1 = K1 , . ., Xt-1 = Kt-1 , = Kt-1, Xt=1}= P {X t+1 | X1 = i }, para toda t = 0, 1, . . y toda
sucesión i, j , K0 , K1 , . . , Ki-1 .
    Se puede demostrar que esta propiedad markoviana es equivalente a establecer una probabilidad condicional de cualquier "evento" futuro dados cualquier "evento " pasado y el estado actual Xi = i , es independiente del evento pasado y sólo depende del estado actual del proceso. Las probabilidades
condicionales P{Xt+1 = j | Xt = i} se llaman probabilidades de transición. Si para cada i y j,
P{ Xt+1 = j | | Xt = i } = p{X1 = j | X0 = i }, para toda t = 0, 1, ....
    Entonces se dice que las probabilidades de transición (de un paso) son estacionarias y por lo general se denotan por pij . Así, tener probabilidades de transición estacionarias implican que las probabilidades de transición no cambian con el tiempo. La existencia de probabilidades de transición (de un paso) estacionarias también implica que, para cada i, j y n (n = 0, 1, 2,...),
P{ Xt+n = j | | Xt = i } = p{Xn = j | X0 = i },
Para toda t = 0, 1, . . . Estas probabilidades condicionales casi siempre se denotan por  y se llaman probabilidades de transición de n pasos. Así,  es simplemente la probabilidad condicional de que la variable aleatoria X, comenzando en el estado i, se encuentre en el estado j después de n pasos ( unidades de tiempo ).
Como las  son probabilidades condicionales, deben satisfacer las propiedades: 
ANÁLISIS DE MARKOV
WB01693_.gif (2469 bytes)
Afin de ilustrar el proceso de Markov presentamos un problema en el que los estados de resultados de actividades son marcas, y las probabilidades de transición expresan la probabilidad de que los consumidores vayan de una marca a otra. Supongamos que la muestra inicial de consumidores se compone de 1 000 participantes distribuidos entre cuatro marcas(A, B, C, D). Una suposición adicional es que la muestra representa a todo el grupo. 
En la siguiente tabla la mayor parte de los clientes que compraron inicialmente la marca A, siguieron con ella en el segundo periodo. No obstante la marca A ganó 50 clientes y perdió 45 con otras marcas. 

Marca
Periodo 1
Numero de Clientes

Ganancias

Perdidas
Periodo 2
Numero de Clientes

A

220

50

45

225

B

300

60

70

290

C

230

25

25

230

D

250

40

35

255

1 000

175

175

1 000
 Esta tabla no muestra la historia completa, sino que necesita un análisis detallado con respecto a la proporción de ganancias y perdidas netas entre las cuatro marcas. Es necesario calcular las probabilidades de transición para las cuatro marcas. Las probabilidades de transición se definen como la probabilidad de que determinada marca, conserve sus clientes. Para determinar lo anterior dividimos se divide el numero de clientes retenidos entre en numero de clientes en el periodo inicial, por ejemplo para la marca A (220- 45=175) se divide 175/220 lo que nos da 0.796, al igual para las otras marcas, obteniendo 0.767(B),0.891(C),0.860(D).
 Para aquellos clientes que cambiaron de marcas , es necesario mostrar las perdidas y ganancias entre las marcas a fin de completar las matriz de probabilidades de transición. De acuerdo con los datos desarrollados, el paso siguiente consiste en convertir el cambio de marcas de los clientes de modo que todas las perdidas y ganancias tomen forma de probabilidades de transición, obteniendo la matriz de probabilidad de transición.
La siguiente tabla nos muestra la matriz de transición final.

A

B

C

D

A

175/220=0.796

40/300=0.133

0/230=0

10/250=0.040

B

20/220=0.091

230/300=0.767

25/230=0.109

15/250=0.060

C

10/220=0.046

5/300=0.017

205/230=0.891

10/250=0.040

D

15/220=0.067

25/300=0.083

0/230=0

215/250=0.860
 La lectura de esta información sería la siguiente:
La marca A retiene 0.796 de sus clientes, mientras que gana 0.133 de los clientes de B, 0.40 de los clientes de D y 0 de los clientes de C.
La administración de mercadotecnia puede tener un gran ventaja de toda esta información que nos pueda arrojar el desarrollo de técnicas como estas, ayudando a la promoción de algunos productos que los necesiten para tener una mejor aceptación entre los consumidores.
Probabilidad de transición estacionaria de n pasos.
    Las ecuaciones de Chapman-Kolmogorov proporcionan un método para calcular estas probabilidades de transición de n pasos : 
    Estas ecuaciones simplemente señalan que al ir de un estado i al estado j en n pasos, el proceso estará en algún estado k después de exactamente m ( menor que n) pasos. Así,
    Es solo las probabilidad condicional de que, si se comienza en el estado i, el proceso vaya al estado k despues de m pasos y después al estado j en n- m pasos.
Los casos especiales de m=1 y m=n-1 conducen a las expresiones
    Para toda i, j, y n de lo cual resulta que las probabilidades de transición de n pasos se pueden obtener a partir de las probabilidades de transición de un paso de manera recursiva. Para n=2, estas expresiones se vuelven : 
Note que las  son los elementos de la matriz P(2) , pero también debe de observarse que estos elementos,  se obtienen multiplicando la matriz de transición de un paso por sí misma; esto es , P(2) = P * P = P2 .
    En términos más generales, se concluye que la matriz de probabilidades de transición de n pasos se puede obtener de la expresión : P(n) = P * P .... P = Pn = PPn-1 = Pn-1 P.
    Entonces, la matriz de probabilidades de transición de n pasos se puede obtener calculando la n-ésima potencia de la matriz de transición de un paso. Para valores no muy grandes de n, la matriz de transición de n pasos se puede calcular en la forma que se acaba de describir, pero cuando n es grande, tales cálculos resultan tediosos y, más aún, los errores de redondeo pueden causar inexactitudes.
Ejemplo :
    Una tienda de cámaras tiene en almacén un modelo especial de cámara que se puede ordenar cada semana. Sean D1, D2, ... las demandas de esta cámara durante la primera, segunda, ... , semana, respectivamente. Se supone que las Di son variables aleatorias independientes e idénticamente distribuidas que tienen una distribución de probabilidad conocida. Sea X0 el número de cámaras que se tiene en el momento de iniciar el proceso, X1 el número de cámaras que se tienen al final de la semana uno, X2 el número de cámaras al final de la semana dos, etc. Suponga que X0 = 3 . El sábado en la noche la tienda hace un pedido que le entregan el lunes en el momento de abrir la tienda. La tienda hace un pedido que le entregan el lunes en el momento de abrir la tienda. La tienda usa la siguiente política ( s, S)1 para ordenar : si el número de cámaras en inventario al final de la semana es menor que s =1 (no hay cámaras en la tienda), ordenar (hasta) S=3. De otra manera, no coloca la orden (si se cuenta con una o más cámaras en el almacén, no se hace el pedido). Se supone que las ventas se pierden cuando la demanda excede el inventario. Entonces, {X1} para t = 0, 1, .. es un proceso estocástico de la forma que se acaba de describir. Los estados posibles del proceso son los enteros 0, 1, 2, 3 que representan el número posible de cámaras en inventario al final de la semana.
 
Así, dado que tiene una cámara al final de una semana, la probabilidad de que no haya cámaras en inventario dos semanas después es 0.283; es decir,  De igual manera, dado que se tienen dos cámaras al final de una semana, la probabilidad de que haya tres cámaras en el almacén dos semanas después es 0.097; esto es, 
  La matriz de transición de cuatro pasos también se puede obtener de la siguiente manera :
P(4) = P4 = P(2) * P(2)
    Así, dado que queda una cámara al final de una semana, 0.282 es la probabilidad de que no haya cámaras en inventario 4 semanas más tarde; es decir,  De igual manera, dado que quedan dos cámaras en el almacén final de una semana, se tiene una probabilidad de 0.171 de que haya tres cámaras en el almacén 4 semanas después; esto es,  
Publicado por en
Etiquetas:

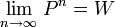
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)